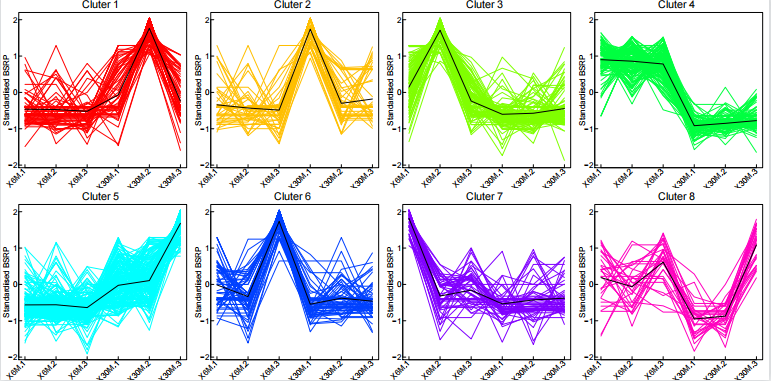
kmeans的介绍参考知乎：https://zhuanlan.zhihu.com/p/78798251?utm_source=qq

优点

  • 容易理解，聚类效果不错，虽然是局部最优， 但往往局部最优就够了；
  • 处理大数据集的时候，该算法可以保证较好的伸缩性；
  • 当簇近似高斯分布的时候，效果非常不错；
  • 算法复杂度低。

缺点

  • K 值需要人为设定，不同 K 值得到的结果不一样；
  • 对初始的簇中心敏感，不同选取方式会得到不同结果；
  • 对异常值敏感；
  • 样本只能归为一类，不适合多分类任务；
  • 不适合太离散的分类、样本类别不平衡的分类、非凸形状的分类。

开始计算

导入数据

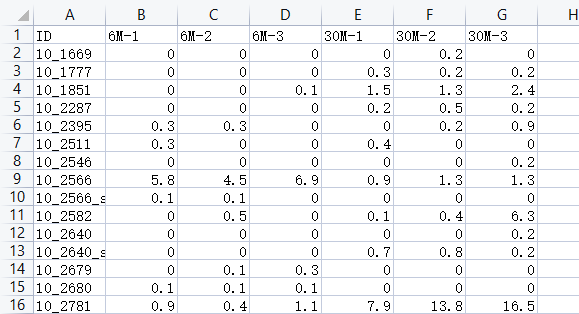
image-20210902100906667

数据格式如上所示，虽然低，但是不要所有的值全为NA，运行代码会报错

NA即为A-G的表达值全部为0

打开R

导入数据：

rm(list = ls())
getwd();
workingDir = “.”;
setwd(workingDir);
options(stringsAsFactors = FALSE);

data=read.csv(“Data_kmeans.csv”)
rownames(data)=data$ID
mean=data[,-1]
data=mean

data_train_matrix=as.matrix(t(#最后再把将标准化的结果再转置，将行变成列，列变成行
scale(#每一列取个均值，取个方差，每个点的值取个均值，取个方差，这样得到的就是标准化的值，但是是对每一列进行的标准化，所以先对数据进行转置，才能满足对函数的要求
t(data)#先进行进行转置，行变成列，列变成行，然后对scale函数对其进行处理
)
)
)

image-20210902105755231

继续

k = 8 #选择分类多少；赋值

#核心代码#
cl=kmeans(data_train_matrix,k,iter.max = 1000)

#data_train_matrix 标准化的数值；#iter.max 需要进行diedai?的次数，首先是随机选择的点进行的聚类，聚完类进行聚类分析的更新以后，再进行聚类，就是迭代，1000个没啥问题，如果1000次觉得少，可以进行增加，10000，十万都可以，这都是没事问题) #k,表示聚类的个数nstart表示聚类的起始个数，如果数据量不大可以不要，这个值可以设置比k值小，也可以大）

#结果输出

write.table(cl$centers,file=”kmeans_center.txt”,
sep = “\t”,quote = F,row.names = T)#quote 是否需要双引号输出，row.name=T 表示输出行的名字

result = data.frame(id=row.names(data),cluster = cl$cluster,data)

write.table(result,file=”kmeans_cluster.txt”,
sep = “\t”,quote = F,row.names = F)

cluster = as.matrix(cl$cluster)

rownum = 2 #画几行，根据图进行调整
colnum = 4 #画几列

pdf(file = “kmeans.pdf”,
width = colnum2,height =rownum2)

par(mfrow=c(rownum,colnum),mar=c(1.5,1.3,1.2,0.4)+0.1, #c,3行4列；mar给出图的四条边；
mgp=c(0.5,0.05,0),tck=0.02,cex.axis=0.8,cex.lab=0.8, #mgp给出轴的坐标标签和轴线条线边距值；tck:刻度值；axis:轴的刻度大小
cex.main=1,font.lab=1,font.axis=1,font.main=1,col.axis=”black”) #cex.main：标题；font.lab=1,font.axis=1,font.main=1：字体；颜色灰色

color=rainbow(k)

for (i in 1:k) {
x=cluster[,1]==i #==判断是否相等
part=data_train_matrix[x,]
len=dim(part)[1]

part=rbind(part,cl$centers[i,])

matplot(t(part),type=’l’,lty=1,col=c(rep(color[i],len),rep(“black”,1)),
axes=F,main=paste(“Cluter”,i,seq=””),xlab = “”,ylab = “Standardised BSRP”,
ylim = range(data_train_matrix))

box(lwd=0.5,col=”black”)
axis(2,lwd=0.5,col=”black”,las=1)
axis(1,1:dim(data_train_matrix)[2],labels = F,lwd=0.5,mgp=c(0,-0.2,0))
text(1:dim(data_train_matrix)[2],par(“usr”)[3]-0.05,srt=45,col=”black”,adj=1,
xpd=T,labels = colnames(data_train_matrix),cex=0.8)

}
dev.off()

最后image-20210902110212276